Radiative Effect of Dust on the Climate of Early Mars
Date:
Project, School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, US
Summer Research Summary Report (pdf)
Abstract
The climate of early Mars was likely strongly influenced by dust with optical properties distinct from those of modern Mars due to a more reducing ancient environment. In this work, we develop a modeling framework to investigate the radiative effects of such dust. We couple Mie scattering theory with a 1D radiative-convective model to assess the impact of airborne dust, and we use the Hapke model to analyze the spectral reflectance of surface regolith systematically. The framework is validated against modern Mars conditions. Our analysis then yields a key physical insight: the surface albedo is as sensitive to particle effective radius as it is to the material’s intrinsic absorption. This result demonstrates that physical texture is as critical as bulk composition, highlighting that a holistic approach considering mineralogical and physical properties is essential for accurately modeling the climates of early Mars and for the spectral interpretation of rocky exoplanets.
Airborne Dust Scattering
I successfully built a generic pipeline to quantify the radiative impact of airborne dust or aerosol particles that is applicable to various planetary atmospheres.
The calculation takes in the particle’s complex refractive index and size distribution, it then utilizes the Mie scattering theory to calculate the single scattering parameters (extinction coefficient $\beta$, single scattering albedo $\varpi$, asymmetry parameter $g$). The code also includes support to: particle radius distribution, height distribution, and mixing of different particles.
PCM_LBL is a 1D radiative-convective model that simulate the climates of planets. It solves for the radiative transfer and thermodynamic structure of a planetary atmosphere. In this project, I modified the scattering version of PCM_LBL to take in the single scattering parameters ($\beta,\varpi,g$) calculated in the Mie code. The shortwave scattering and absorption, as well as longwave absorption by the dust, are included.
Surface Regolith Albedo
I conducted investigation to several theories concerning particulate media reflectance, including the Shkuratov model, the Hapke model, and the Mishchenko model. In the process, I came up with some critical assessment towards the Shkuratov model. After considering credibility and accessibility, we decided to use the Hapke model for the following work.
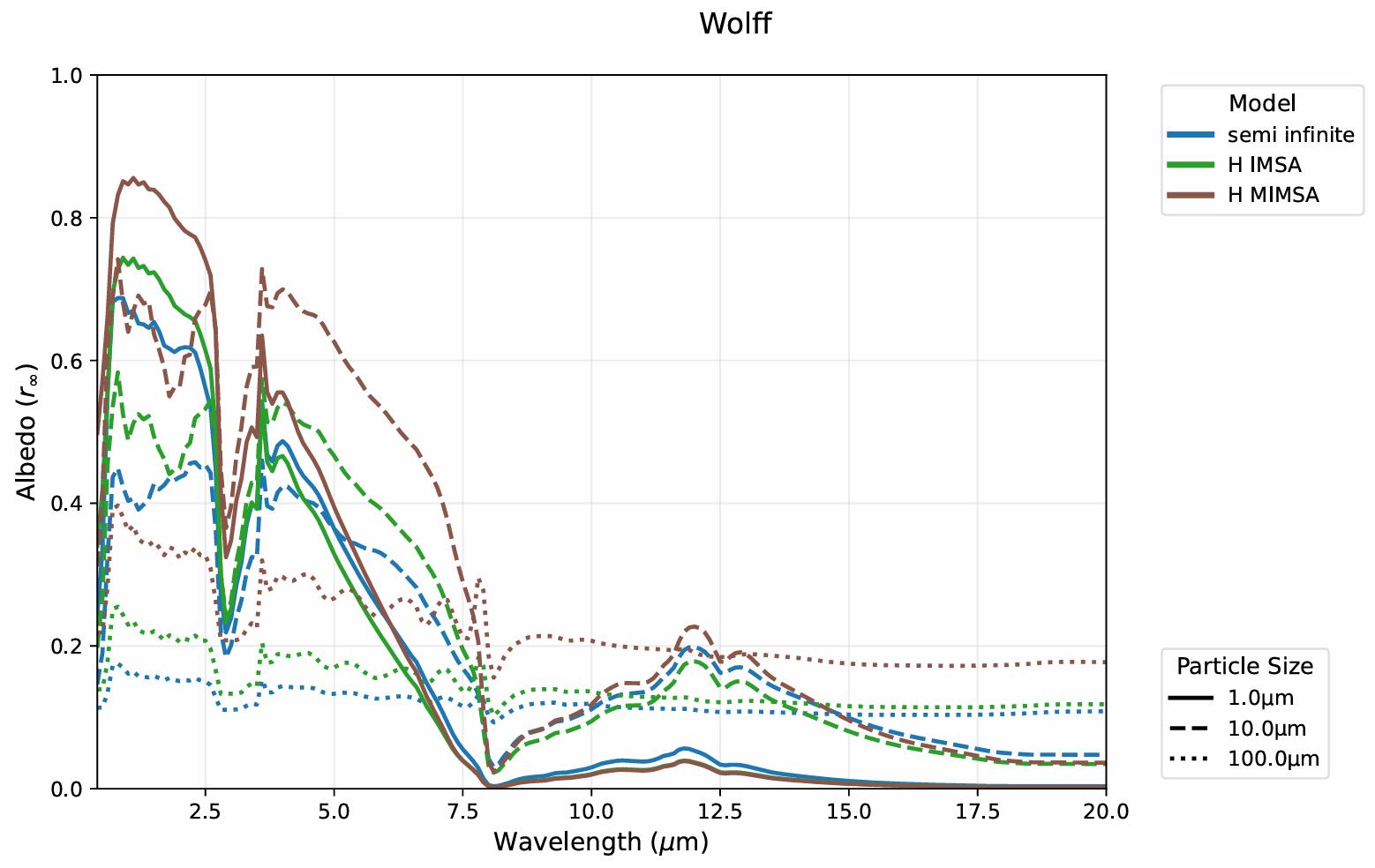
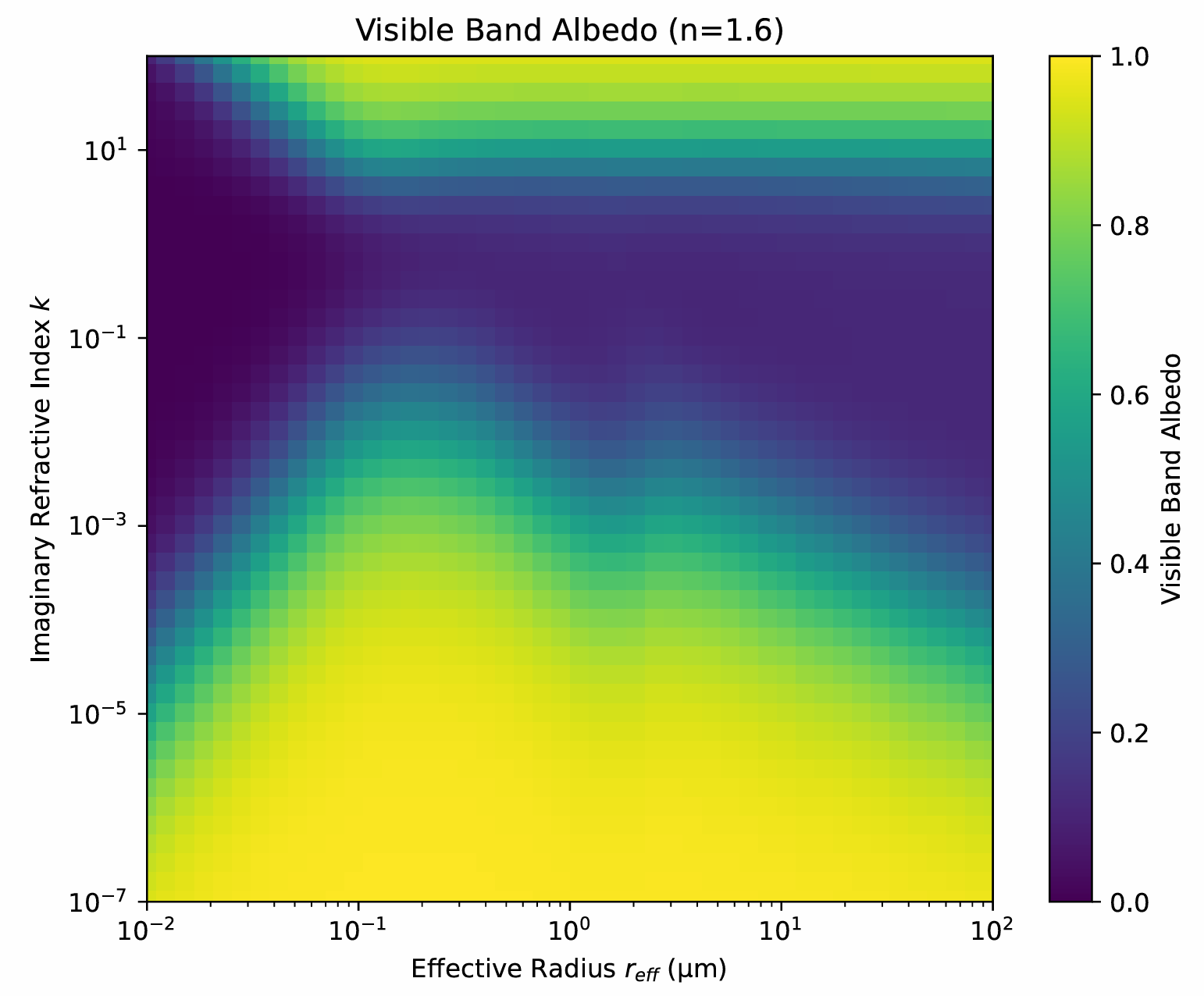
Fig. 2 (b) can be used to illustrate how particle size affects the albedo. From the figure, we can see that for the visible band and typical range of $k,r_{eff}$ ($k<10^0, r_{eff}>10^0\mu\text{m}$), we generally have the albedo larger for smaller $k$ and smaller $r_{eff}$. The impact of particle size is of a comparable order of magnitude to that of $k$. This stresses the importance of determining the radius distribution of the regolith in practical calculations.
Future Work
Comparison with Lab Measurements
To rigorously validate the Hapke model, a key future direction is to perform detailed laboratory measurements. This work will involve preparing rock samples with high-resolution particle size distributions and using a spectrometer to measure their reflectance. This will provide crucial ground-truth data to test and refine the model’s ability to predict macroscopic albedo from the fundamental physical properties of the particles.
Implications for Early Mars
My research highlights that particle size can be as influential as chemical composition in determining planetary albedo, challenging the use of a single, fixed value in early Mars climate models. A crucial next step is to place physical constraints on plausible particle sizes by considering various weathering and fluvial processes on early Mars. This will enable a more dynamic and realistic representation of both surface and airborne dust, refining our understanding of the early Martian climate.
Implications for Exoplanets
The principles of how surface properties shape a planet’s spectrum extend far beyond Mars, with direct applications for exoplanet characterization. By accurately modeling the expected spectra of various bare-rock surfaces, we can establish a critical baseline for astronomical observations. A significant deviation from this baseline, such as an unexpectedly high albedo, could then serve as compelling indirect evidence for the presence of an atmosphere.
Other Interesting Stuff
Colorimetry - From Spectrum to Color
Human eyes have three types of cone cells, each of which has a distinct spectral response function to lights of different wavelengths. The response functions of these three cone cells are $L(\lambda), M(\lambda), S(\lambda)$, representing long to short wavelength. By integrating the spectrum using these corresponding functions as weighing functions, we can get the so-called LMS values, which can be converted into RGB values that can be displayed on a screen.


For more information, please refer to this summary report for my 2025 summer research!
